Programmation en Python, classe de Terminale

Ce qui suit servira essentiellement à l'enseignant de mathématiques. La présence d'un [PAA] dans le texte fait référence au livre PAA ci-dessous, dont la lecture peut débuter par l'enseignant tout de suite, et par l'élève en classe Terminale pour se poursuivre dans le Supérieur. L'élève en classe de Terminale pourra consulter le Mémento en pdf.

PAA

Que dit le B.O. sur le programme de Terminale ?

Les connaissances à acquérir

Le texte officiel du B.O. dit bien qu'il n'y a pas de notions nouvelles (comprenez de nouveaux types de données ou de nouvelles techniques de programmation) en Terminale. Il s'agit donc dans un premier temps d'utiliser le niveau de langage de Première pour aborder des algorithmes un peu plus délicats Je pense raisonnable d'introduire les ensembles dans le thème dénombrement et probabilités, ainsi que (moins important) les dictionnaires : collections de couples clé/valeur.

Python fournit des types de données set et dict à part entière pour ces objets moins linéaires que les listes, mais à vrai dire on peut s'en passer en construisant à la main (par l'enseignant ou l'élève) des équivalents à partir des listes, quitte à ne pas avoir la même efficacité ou simplicité d'écriture.

Le B.O. ne parle pas non plus de programmation par récurrence alors qu'il cite - parmi les techniques de démonstration - le raisonnement par récurrence (en situation, mais c'est la même chose en programmation : il ne s'agit pas d'étudier les fondements de la récursivité). A mon humble avis, il faut montrer quelques fonctions utilisant la récurrence en Terminale spé maths, notamment pour les suites, le dénombrement ou l'arithmétique...

1. Révisions de Première

Il est indispensable de faire au moins deux séances de révision, en reprenant une galerie de fonctions typiques avec ou sans résultat, illustrant les points essentiels du programme de Première : affichages avec print, paramètres et arguments, variables locales et globales, conditionnelle, boucles, listes et compréhensions, graphisme de la tortue. Les types étudiés en Première étaient int, float, bool, list et un peu str. Il est probable, au vu de leur expérience variable dans la pratique et l'enseignement de la programmation, que tous les enseignants n'auront pas traités dans les mêmes détails certaines parties de Seconde et Première.

2. Les ensembles (`set`) de Python [PAA §5.7]

Le vocabulaire naïf des ensembles est présent au lycée, réduit à la notation en compréhension {x ∈ E : propriete(x)}, aux opérations ensemblistes (réunion, etc), et aux assertions avec quantificateurs ∀ et ∃ (quitte à les rédiger en langage naturel).

Ces ensembles ne pouvaient échapper à la programmation et Python propose un type set qui fait de son mieux pour modéliser ces objets mathématiques historiquement sulfureux. Un ensemble se note comme en maths {3, 7, 4, 8} sans ordre et sans répétition. Un ensemble n'est pas une séquence : ses éléments ne sont pas numérotés.

>>> E = {3, 7, 4, 3, 8}       # ou bien set([3, 7, 4, 3, 8])
>>> (E, len(E), type(E))      # l'ensemble E, son cardinal et sa classe (type)
({8, 3, 4, 7}, 4, <class 'set'>)   # sans répétition et en ordre apparemment quelconque
>>> 4 in E                    # 3 ∈ 4 ? Algorithme beaucoup plus efficace qu'avec les listes !
True
>>> set()                     # Aïe, {} n'est pas un ensemble mais un dictionnaire !
set()                         # ← c'est lui l'ensemble vide
>>> E == {7, 3, 8, 4}         # les mêmes éléments à une permutation près
True

Les opérations élémentaires sont la réunion E | F (la barre verticale signifie "ou" en informatique), l'intersection E & F et la différence E - F :

>>> {4,3,5} | {4,8,2,3}     # {4,3,5} ∪ {4,8,2,3}
{2, 3, 4, 5, 8}
>>> {4,3,5} & {4,8,2,3}     # {4,3,5} ∩ {4,8,2,3}
{3, 4}
>>> {4,3,5} - {4,8,2,3}     # {4,3,5} \ {4,8,2,3}
{5}

Les ensembles sont des objets mutables. On ajoute sur place un objet x à l'ensemble E avec E.add(x), on supprime x avec E.remove(x), et on supprime un élément quelconque avec E.pop() qui retourne l'élément supprimé (axiome du choix). On ne confondra pas E.add(x) - qui fait muter E - avec E = E | {x} qui construit un nouvel ensemble !

NB. i) En Python, on ne peut pas mettre n'importe quoi dans un ensemble, seulement des objets non mutables (nombres, booléens, chaînes, tuples, fonctions, mais pas de listes ou d'ensembles !).
ii) Donc pas d'ensemble d'ensembles (pas d'ensemble des parties !)... Il faudrait passer par un autre type d'ensemble gelé frozenset que l'on se gardera d'aborder [PAA p. 89]. Ou bien simuler les ensembles avec des listes [PAA exo 11.96].

2.1 Mieux : construire ses propres ensembles (pEns)

L'enseignant peut faire le choix [basé sur PAA exo 11.96] de voir les listes d'éléments distincts et sans ordre spécifié comme des pseudo-ensembles (pEns). Il pourra demander aux élèves de programmer tout ou partie parmi : appartenance, réunion, intersection, différence, inclusion, égalité, produit cartésien et ensemble des parties, le dernier exemple étant particulièrement instructif (par récurrence), tout comme la programmation de la liste des combinaisons et arrangements à p éléments d'un pEns à n éléments.

ATTENTION. Des pièges subtils sont liés à l'utilisation de .append que l'on évitera d'utiliser sur un paramètre de fonction ! Un exemple de fonction qui ne tombe pas dans le piège :

def union(E,F):          # réunion itérative de pEns
    res = [x for x in E] # copie de E tout entier, et NON res = E
    for x in F:
        if x not in E:   # ajout d'une partie seulement de F
            res.append(x)
    return res

>>> union([4,3,5],[4,8,2,3])      # réunion
[4, 3, 5, 8, 2]                   # ordre non spécifié

Premier bémol : mieux vaut se limiter à des pEns d'entiers si l'on veut avoir une inclusion entre pEns facile à programmer (car == ne fonctionnera plus si les éléments sont eux-mêmes des pEns !).

Second bémol : l'efficacité du test d'appartenance à un pEns réalisé par une liste sera médiocre car linéaire en la longueur de la liste, sauf à trier régulièrement cette dernière pour avoir un coût logarithmique (par dichotomie). Mais quid alors si la liste contient des objets de divers types ? Il faut clairement, vu le temps imparti, faire le choix de la simplicité au détriment de l'efficacité, qui viendra après le Bac.

Comme autre exemple, programmons par récurrence la fonction parties(E) prenant un pEns E et retournant le pEns des parties de E. Notez que le programme se déroule comme la preuve par récurrence que parties(E) contient 2ⁿ éléments si E comporte n éléments. Jolie symbiose entre les maths pures et la programmation !

def parties(E):             # E est un pEns
    if len(E) == 0: return [[]]    # 2**0 == 1
    x = E[0]                # j'isole un élément de E et je considère le reste
    reste = [E[i] for i in range(1,len(E))]   # <==> E[1:] si les élèves connaissent
    HR = parties(reste)     # je pose calmement mon hypothèse de récurrence
    return HR + [P + [x] for P in HR]         # réunion disjointe... 2ⁿ = 2^n-1 + 2^n-1

>>> parties([1,2,3])
[[], [3], [2], [3, 2], [1], [3, 1], [2, 1], [3, 2, 1]]

NB. Le module itertools de Python contient d'utiles fonctions sur les listes pour faire du dénombrement (produit cartésien, combinaisons, permutations, etc) mais il utilise souvent des itérateurs hors-programme. Exemple avec permutations dont le résultat est un itérateur (objet que l'on peut parcourir avec une boucle for..in..). Mais lors d'une activité, l'enseignant peut fournir aux élèves des fonctions analogues cachant les itérateurs :
>>> from itertools import permutations # [PAA ligne 804] >>> permuts = lambda L: list(permutations(L)) >>> permuts([1,2,3]) [(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)]

3. Les dictionnaires (`dict`) de Python [PAA §5.8]

La structure de dictionnaire a été inventée pour stocker des couples (clé,valeur) que Python écrit cle:valeur. Un dictionnaire n'est pas une séquence : ses éléments ne sont pas numérotés, mais accessibles en fournissant la clé. Toutes les clés doivent être distinctes et non mutables (entiers, chaînes, tuples, ensembles). Les valeurs par contre sont quelconques.

>>> dico = {1:'one', 2:'two', 3:'three'}
>>> (len(dico), type(dico))
(3, <class 'dict'>)
>>> 2 in dico                # le dico contient-il la clé 2 ?
True
>>> dico[2]                  # accès clé → valeur, pas l'inverse !
'two'
>>> dico['trois'] = 'three'  # ajout d'une nouvelle clé:valeur
>>> dico
{1:'one', 2:'two', 3:'three', 'trois':'three'}
>>> for k in dico:           # on boucle sur les clés k !
        if dico[k] == 'three': print(k, end=' ')
3 trois
>>> [k for k in dico if dico[k] == 'three']
[3, 'trois']

Les valeurs sont accessibles en bouclant sur dico.values() qui retourne un itérateur :

>>> set(dico.values())       # l'ensemble des valeurs
{'one', 'two', 'three'}

Une application importante des dictionnaires : ils peuvent jouer le rôle de mémoire privée d'une fonction, lui permettant de se souvenir des calculs déjà effectués. Prenons l'exemple du coefficient binomial C(n,p) dont une définition par récurrence serait :

def C(n,p):                     # on suppose 0 <= p <= n entiers
    if (p == 0) or (n == p):    # les bords du triangle de Pascal
        return 1
    return C(n-1,p) + C(n-1,p-1)

>>> C(5,3)
10

Hélas, le nombre de mains au bridge C(52,13) n'est pas accessible ! Cette fonction va passer son temps à refaire les mêmes calculs. Il suffit de lui greffer un cerveau privé MEM qui contiendra des neurones [(n,p),v] exprimant que le calcul de C(n,p) a été déjà effectué et a donné le résultat v. Et MEM sera bien entendu un dictionnaire.

MEM = []                             # elle serait mieux en locale !

def C(n,p):                          # [voir corrigé de PAA exo 11.100]
    global MEM                       # cours de Première
    if (p==0) or (n==p): return 1    # bords du triangle de Pascal
    "si MEM contient un neurone [(n,p),v] alors retourner v"  # à vous !
    v = C(n-1,p) + C(n-1,p-1)        # sinon on fait le calcul,
    "et on stocke un nouveau neurone dans MEM"                # à vous !
    return v
    
# C(52,13) donne 635013559600 en 0.001 sec.
# et MEM comporte alors 507 neurones (on a échangé du temps contre de l'espace).

Un autre exemple d'utilisation des dictionnaires : les graphes dont une représentation par listes d'adjacence retarde l'arrivée des matrices hors-programme. Le graphe orienté ci-dessous serait représenté par le dictionnaire : SUCC = {1:[2,4], 2:[4], 3:[1,2]}, les successeurs du sommet 3 étant obtenus par SUCC[3].

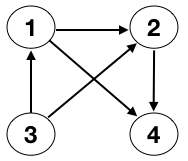
ou encore les chaînes de Markov (certains graphes orientés dont les arêtes sont pondérées par des probabilités de transition de sommet à sommet) qui pourraient être une activité dans le cadre du cours sur les variables aléatoires. Voir par exemple Maths Expertes (Terminale).

4 La Récurrence en programmation [PAA §2.23]

Sujet à controverse. Faut-il enseigner le principe de récurrence en maths mais faire l'impasse sur la programmation par récurrence ? A mon humble avis (IMHO), non. En effet, une fois le concept de récurrence assimilé, il n'y a aucune raison qu'une fonction Python ne puisse faire appel à elle-même, et en profiter de temps en temps ne pourra que renforcer la compréhension de la récurrence. Ayant longtemps enseigné dans le supérieur, je peux dire qu'elle est très mal assimilée !

Ceci dit, il y a un bémol. Comme d'autres langages (pas tous), Python pose certaines limitations - ou plutôt refuse certaines optimisations - qui n'ont plus trop lieu d'être mais le fait est là.

⦿ Quel est le point commun entre la récurrence en maths et son analogue en programmation ? C'est l'intention formidable de réduire un problème portant sur une donnée N au même problème portant sur une donnée N' < N. Et de telle sorte que la transformation N ↦ N' converge en un nombre fini d'étapes vers une donnée N₀ assez petite pour que le problème soit immédiatement résoluble. Typiquement N est un entier naturel, N'=N-1 et N₀=0. Le matheux construit le texte d'une preuve, le programmeur construit le texte d'une fonction. Chacun d'eux pose une Hypothèse de Récurrence sur N'.

--------------------------------------------         -------------------------------
THEOREME : Pour tout n entier naturel,               def somcar(n):   # n entier ≥ 0
1²+2²+3²+...+n²=n(n+1)(2n+1)/6                            if n=0: return 0 
PREUVE : Si n = 0, évident (0=0). Sinon,                 return somcar(n-1) + n*n
supposons la relation vraie pour n-1
et montrons qu'elle est vraie pour n. Etc.
--------------------------------------------         -------------------------------

NB. Les livres de maths du secondaire passent plutôt de n à n+1, héritage d'un temps où la programmation n'existait pas. N'est-il pas temps de se mettre à jour ?...

⦿ Qu'est-ce qui différencie la récurrence en programmation de son analogue en maths ? La présence d'une machine bien entendu, et de l'état de l'art dans la technologie des machines et des langages. Dans la dernière ligne de la fonction somcar, l'addition ne peut se faire qu'après le calcul de somcar(n-1). Cette addition sera donc mise en attente (dans une pile), ainsi que toutes celles qui suivront, et toutes ces additions empilées ne seront effectuées qu'à partir du point bas de la récurrence, sur N₀=0. Il faut donc de la mémoire, qui hélas au lieu de dépendre de la mémoire effective de la machine (comme avec la précision infinie des entiers par exemple), est fixée à une taille très limitée qui va poser des problèmes si n est grand (couramment de l'ordre de 1000, mais est-ce grand ?). Il est possible d'augmenter à la main la mémoire allouée à la pile ([PAA §2.23.2]), il est aussi possible d'être très astucieux et d'outrepasser ces limitations ([PAA exo 11.132]), mais tout ceci fait un peu bidouille... Tel est l'état de l'art en Python (ou Java), il faut faire avec.

⦿ Il existe une autre différence que les matheux n'ont jamais perçue et pour cause, puisque la notion de boucle leur est inconnue. Considérons l'algorithme d'Euclide pour le PGCD dans sa version naturelle (lisez mathématique) : par récurrence.

def pgcd(a,b):             # a et b entiers naturels
    if b == 0: return a
    return pgcd(b,a % b)   # récurrence terminale ou quasi-itérative ([PAA] §2.23.2)

Le nombre de divisions est faible : logarithmique en min(a,b) - théorème de Lamé - donc la pile ne posera pas de problème. Plus intéressante est l'observation que l'appel à la fonction pgcd en réalité ne sert à rien. Il y a un simple remplacement du couple (a,b) par le couple (b,a % b). Un texte équivalent devrait donc être :

def pgcd(a,b):             # a et b entiers naturels
    while b != 0:
        (a,b) = (b,a % b)
    return a

Cette équivalence opérationnelle est fausse en Python, qui empile inutilement les calculs intermédiaires alors que la récurrence est terminale. Cela ne pose pas de problème ici car la pile ne monte pas trop, mais s'avère critique pour traiter une longue liste par récurrence, ou calculer une grande factorielle.

Alors, que faire ? Deux pas en avant et un pas en arrière. On montre la programmation par récurrence aux élèves sur des cas simples (factorielle, somme d'entiers, suites, ensembles, dénombrement) et on met le doigt sur la possibilité d'explosion de la pile. Il me semble jouable, dans le cadre d'une activité, de montrer la technique de mémorisation du §3 analogue au dépôt d'un cookie lors de la visite d'une page Web. Dans le cadre des listes, il faut au maximum utiliser les bons outils de Python que sont les compréhensions, qui évitent souvent des boucles un peu pataudes.

En rédigeant une fonction par récurrence, il sera toujours sain de montrer une version avec boucle, lorsque la boucle vient facilement. On négociera entre l'efficacité et la facilité de rédaction.

Vous trouverez dans [PAA] des exercices fondamentaux sur la récurrence, comme §11.19, §11.20f, §11.22, §11.24, §11.40, §11.41, §11.44, §11.66, §11.76, §11.78, §11.92, etc.